Primitives Reference

LDraw Primitives Reference

This page is a source of reference for the LDraw primitives in the \LDraw\p directory. Primitives are defined as highly re-usable components of LEGO parts modelled for LDraw. They serve several purposes :

• To speed up parts authoring by providing a library of components which can be incorporated into several parts
• To allow rendering software to make substitutions of curved components

Within this reference material the available primitives are categorised into:

Each section contains an overview of the characteristics common to all primitives within that category. Primitives are grouped into classes within each category - one class of primitive serving a similar purpose at different sizes or resolutions. For each class of primitive, a brief description of the purpose of the primitive is provided, with notes on its co-ordinate origin, default size and rules for scaling. A list of the available primitives is shown.

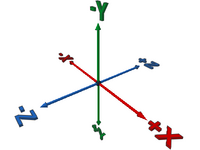
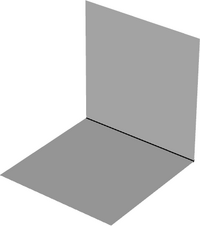
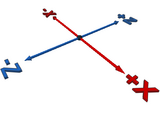
An understanding of the orientation of the co-ordinate axes is essential for authoring a part for LDraw. For reference within this page the axes and their direction is shown in this diagram.

Rectilinear primitives

These rectilinear elements may be scaled in the {x}, {y} and {z} dimensions to make elements of any size. For example

1 16    0 0 0    40 0 0    0 1 0    0 0 20    rect.dat

would generate a 80LDu x 40LDu rectangle in the {x,z} plane.

Although the default orientation of the rect.dat primitive is in the {x,z} plane the LDraw language allows for this to be transformed

1 16    0 0 0    0 1 0    40 0 0    0 0 20    rect.dat

would generate a 80LDu x 40LDu rectangle in the {y,z} plane.

1 16    0 0 0    40 0 0    0 0 20    0 1 0    rect.dat

would generate a 80LDu x 40LDu rectangle in the {x,y} plane.

Two dimensional

triangle.dat	Triangle with all edges
	This primitive represents a right angled isosceles triangle in the {x,z} plane and the three edges that bound it. Its origin is at the tip of the right angle and by default has a size of 1LDu in each of the {x} and {z} dimensions. To avoid matrix arithmetic problems in some renderers, the third dimension ({y} in the default orientation) must be given a non-zero scaling factor. 1 16    0 0 0    5 0 0    0 1 0    0 0 20    triangle.dat
rect.dat	Rectangle with all edges
	This primitive represents a rectangle in the {x,z} plane and the four edges that bound it. Its origin is at its centre and by default has a size of 2LDu in each of the {x} and {z} dimensions.
rect3.dat	Rectangle with 3 edges
	This primitive represents a rectangle in the {x,z} plane but excludes one edge {-z}. Its origin is at its centre and by default has a size of 2LDu in each of the {x} and {z} dimensions.
rect2p.dat	Rectangle with 2 parallel edges
	This primitive represents a rectangle in the {x,z} plane but excludes two parallel edges ({+x} and {-x}). Its origin is at its centre and by default has a size of 2LDu in each of the {x} and {z} dimensions.
rect2a.dat	Rectangle with 2 adjacent edges
	This primitive represents a rectangle in the {x,z} plane but excludes two adjacent edges ({-x} and {-z}). Its origin is at its centre and by default has a size of 2LDu in each of the {x} and {z} dimensions.
rect1.dat	Rectangle with 1 edge
	This primitive represents a rectangle in the {x,z} plane but include only the one {+x} edge. Its origin is at its centre and by default has a size of 2LDu in each of the {x} and {z} dimensions.
recte3.dat	Empty rectangle with three edges
	This primitive represents three edges of a rectangle in the {x,z} plane. Its origin is at its centre and by default has a size of 2LDu in each of the {x} and {z} dimensions.
recte4.dat	Empty rectangle with all edges
	This primitive represents the four edges of a rectangle in the {x,z} plane. Its origin is at its centre and by default has a size of 2LDu in each of the {x} and {z} dimensions.

Three dimensional

box.dat	Cuboid with all faces and edges
	This primitive is used to define a cuboid. Its origin is the centre of the cuboid and by default has a size of 2LDu in each of the three dimensions.
box0.dat	Cuboid with no faces and edges
	This primitive is used to define the frame a cuboid. Its origin is the centre of the cuboid and by default has a size of 2LDu in each of the three dimensions.
box5.dat	Cuboid with 5 faces and all edges
	This primitive represents a cuboid missing the top {-y} face. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
box5-1.dat	Cuboid with 5 faces without 1 edge
	This primitive represents a cuboid missing the top {-y} face and one edge {-z} of that. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
box5-2p.dat	Cuboid with 5 faces without 2 parallel edges
	This primitive represents a cuboid missing the top {-y} face and two of the four edges surrounding that. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
box5-4a.dat	Cuboid with 5 faces without top edges
	This primitive represents a cuboid missing the top {-y} face and the four edges surrounding that. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
box5-12.dat	Cuboid with 5 faces missing all edges
	This primitive represents a cuboid missing the top {-y} face and all edges. Its primary use is for sticker parts. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
box4.dat	Cuboid with 4 parallel faces and all edges
	This primitive represents a cuboid missing the top {-y} and bottom {+y} faces. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
box4o4a.dat	Cuboid with 4 parallel faces without bottom edges
	This primitive represents a cuboid missing the top {-y} and bottom {+y} faces, and missing the edges of the bottom face. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
box4o8a.dat	Cuboid with 4 parallel faces without top and bottom edges
	This primitive represents a cuboid missing the top {-y} and bottom {+y} faces, and missing the edges of the top and bottom face. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
box4t.dat	Cuboid with 4 adjacent and all edges
	This primitive represents a cuboid missing the top {-y} and front {-z} faces, but with all its edges. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
box4-1.dat	Cuboid with 4 adjacent faces missing 1 edge
	This primitive represents a cuboid missing the top {-y} and front {-z} faces and the edge between those faces. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
box4-2p.dat	Cuboid with 4 faces without two opposite top edges
	This primitive represents a cuboid missing the top {-y} and bottom {+y} faces, and missing two edges of the top face - the intersection of the two missing faces and the opposite edge. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
box4-3p.dat	Cuboid with 4 faces without three parallel edges
	This primitive represents a cuboid missing the top {-y} and bottom {+y} faces and missing three edges of the missing faces. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
box4-4a.dat	Cuboid with 4 adjacent faces missing 4 edges
	This primitive represents a cuboid missing the top {-y} and front {-z} faces and all the edges of the missing front face. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
box4-5a.dat	Cuboid with 4 adjacent faces missing 5 edges
	This primitive represents a cuboid missing the top {-y} and front {-z} faces and all the edges at the top and the bottom of the missing front face. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
box4-7a.dat	Cuboid with 4 adjacent faces missing 7 edges
	This primitive represents a cuboid missing the top {-y} and front {-z} faces and all the edges of both missing faces. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
box4-12.dat	Cuboid with 4 adjacent faces missing all edges
	This primitive represents a cuboid missing the top {-y} and front {-z} faces and excludes all the edges. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
box3-3.dat	Cuboid with 3 adjacent faces missing 3 edges
	This primitive represents a cuboid missing the top {-y} and bottom {+y} faces, and missing three edges of the missing faces. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
box3-5a.dat	Cuboid with 4 adjacent faces missing 4 edges
	This primitive represents a cuboid missing the top {-y}, front {-z} and left {-x} faces and includes the three internal edges and the outer edges except those on the left {-z}. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x}, {y} and {z} dimensions.
box3-7a.dat	Cuboid with 3 adjacent faces missing 7 adjacent edges
	This primitive represents a cuboid missing the top {-y}, front {-z} and left {-x} faces and includes the three internal edges but only the outer edges at the top (-y). Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x}, {y} and {z} dimensions.
box3-9a.dat	Cuboid with 3 adjacent faces missing 9 adjacent edges
	This primitive represents a cuboid missing the top {-y}, front {-z} and left {-x} faces and includes only the three internal edges. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x}, {y} and {z} dimensions.
box3-12.dat	Cuboid with 3 adjacent faces missing all edges
	This primitive represents a cuboid missing the top {-y}, front {-z} and left {-x} faces but excludes all edges. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x}, {y} and {z} dimensions.
box3u2p.dat	Cuboid with 3 faces missing 2 edges
	This primitive represents a cuboid missing the top {-y} and left {-x} and right {+x} faces and excludes the top edges of the left {-x} and right {+x} faces. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
box3u4p.dat	Cuboid with 3 faces missing 4 parallel edges
	This primitive represents a cuboid missing the top {-y} and left {-x} and right {+x} faces and excludes the topand bottom edges of the left {-x} and right {+x} faces. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
box3u4a.dat	Cuboid with 3 adjacent faces missing all edges
	This primitive represents a cuboid missing the top {-y} and left {-x} and right {+x} faces and excludes the edges of the missing top face. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
box3u5p.dat	Cuboid with 3 faces missing 5 edges
	This primitive represents a cuboid missing the top {-y} and left {-x} and right {+x} faces and excludes the top edge of the left {-x} face and all edges of the right {+x} face. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
box3u6.dat	Cuboid with 3 faces missing 6 edges
	This primitive represents a cuboid missing the top {-y} and left {-x} and right {+x} faces and excludes the top and bottom edges of the right {+x} face and all edges of the left {-x} face. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
box3u6a.dat	Cuboid with 3 faces missing 4 adjacent and 2 parallel edges
	This primitive represents a cuboid missing the top {-y} and left {-x} and right {+x} faces and excludes all the top edges and the bottom edges of the missing faces. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
box3u7a.dat	Cuboid with 3 faces missing 7 adjacent edges
	This primitive represents a cuboid missing the top {-y} and left {-x} and right {+x} faces and excludes the edges of the missing top (-y) and right (+x) faces. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
box3u8p.dat	Cuboid with 3 faces missing 8 edges (in two parallel groups)
	This primitive represents a cuboid missing the top {-y} and left {-x} and right {+x} faces and excludes all the edges of the left {-x} and right {+x} faces. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
box3u10p.dat	Cuboid with 3 faces in a 'U' shape, missing 10 edges (all except those between the faces)
	This primitive represents a cuboid missing the top {-y} and left {-x} and right {+x} faces and excludes all the edges except the two betweenthe faces. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
box3u12.dat	Cuboid with 3 parallel faces missing all edges
	This primitive represents a cuboid missing the top {-y} and left {-x} and right {+x} faces and excludes all the edges. Its origin is the centre of the (missing) top face and by default has a size of 2LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
boxjcyl4.dat	Box truncated by cylinder
	This suite of primitives are used to model the intersection between a box and cylinders of different radii. The box has a fixed width of 2LDu and the cylinder radius is denoted by the r in the filename. Currently available primitives : Regular resolution (boxjcylr) : 4
box2-5.dat	Cuboid with 2 adjacent faces missing 5 edges
	This primitive represents a cuboid missing the top {-y}, front {-z}, left {-x} and right {+x} faces and excludes all the edges which do not bound the included faces. Its origin is the centre of the cuboid and by default has a size of 2LDu in each of the {x}, {y} and {z} dimensions.
box2-7.dat	Cuboid with 2 adjacent faces missing 7 edges
	This primitive represents a cuboid missing the top {-y}, front {-z}, left {-x} and right {+x} faces and excludes all the edges except that at the join between the two faces and those along the left {-x} and right {+x} sides. Its origin is the centre of the cuboid and by default has a size of 2LDu in each of the {x}, {y} and {z} dimensions.
box2-9.dat	Cuboid with 2 adjacent faces missing 9 edges (all except those connected to the {+x}, {+y}, {+z} vertex)
	This primitive represents a cuboid missing the top {-y}, front {-z}, left {-x} and right {+x} faces and excludes all the edges except that at the join between the two faces and those along the right {+x} sides. Its origin is the centre of the cuboid and by default has a size of 2LDu in each of the {x}, {y} and {z} dimensions.
box2-9p.dat	Cuboid with 2 adjacent faces missing 9 edges (all except three parallel edges)
	This primitive represents a cuboid missing the top {-y}, front {-z}, left {-x} and right {+x} faces and excludes all the edges except that at the join between the two faces and those parallel to that. Its origin is the centre of the cuboid and by default has a size of 2LDu in each of the {x}, {y} and {z} dimensions.
box2-11.dat	Cuboid with 2 adjacent faces missing 11 edges
	This primitive represents a cuboid missing the top {-y}, front {-z}, left {-x} and right {+x} faces and excludes all the edges except that at the join between the two faces. Its origin is the centre of the cuboid and by default has a size of 2LDu in each of the {x}, {y} and {z} dimensions.
tri3.dat	Right-angled triangular prism with 3 faces
	This primitive represents a triangular prism missing the top {-y} and bottom {+y} faces but including all edges. The left {-x} and front {-z} faces are perpendicular. Its origin is the right-angle corner of the (missing) top face and by default has a size of 1LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
tri3-1.dat	Right-angled triangular prism with 3 faces
	This primitive represents a triangular prism missing the top {-y} and bottom {+y} faces and excludes the top edge of the hypotenuse. Its origin is the right-angle corner of the (missing) top face and by default has a size of 1LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
tri3-3.dat	Right-angled triangular prism missing 3 faces
	This primitive represents a triangular prism missing the top {-y} and bottom {+y} faces and excludes all top edges. Its origin is the right-angle corner of the (missing) top face and by default has a size of 1LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
tri3a1.dat	Right-angled triangular prism with 3 adjacent faces missing 1 edge
	This primitive represents a triangular prism missing the top {-y} face, the face at the hypotenuse as well as the top edge at the hypotenuse. Its origin is the right-angle corner of the (missing) top face and by default has a size of 1LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
tri3a3.dat	Right-angled triangular prism with 3 adjacent faces missing 3 edge
	This primitive represents a triangular prism missing the top {-y} face, the face at the hypotenuse and excludes all top edges. Its origin is the right-angle corner of the (missing) top face and by default has a size of 1LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
tri3a4	Right-angled triangular prism with 3 adjacent faces missing 4 adjacent edges
	This primitive represents a triangular prism missing the top {-y} face, the face at the hypotenuse and excludes all edges at the hypotenuse. Its origin is the right-angle corner of the (missing) top face and by default has a size of 1LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
tri3u1.dat	Right-angled triangular prism with 3 faces missing 1 edge
	This primitive represents a triangular prism missing the left {-x} and front {-z} faces. Its origin is the right-angle corner of the top face and by default has a size of 1LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
tri3u3.dat	Right-angled triangular prism with 3 faces missing 3 edges
	This primitive represents a triangular prism missing the left {-x} and front {-z} faces, the edge where they would join and one edge of each of the triangles. Its origin is the right-angle corner of the top face and by default has a size of 1LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.
tri4.dat	Right-angled triangular prism with 2 square faces and 2 triangular faces
	This primitive represents a triangular prism missing the face at the hypotenuse. Its origin is the right-angle corner of the top face and by default has a size of 1LDu in each of the {x} and {z} dimensions and 1LDu in the {y} dimension.

Curved primitives

LDraw represents curved surfaces as polygons. For circular components two series of primitives are provided.

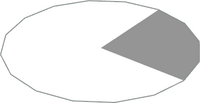
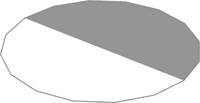
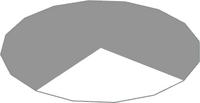
All the circular primitives are orientated in the {x,z} plane with their origin at the centre of the circle and a default radius of 1 LDu. Primitives are provided for complete circles and for commonly used fractions of a complete circle. Where the naming convention includes a prefix of the form n-f this indicates the fraction (n/f) of the circle drawn by the primitive. Where this fraction is less than an entire circle, the primitive starts at {+x,0} and progresses in a conterclockwise direction when viewed from above {-y}.

To avoid rounding errors, it is preferable to use existing fractional circular primitives, or create a new primitive, rather than rotate an existing primitive by anything other than 90 or 180 degrees. For example, use 3-16XXXX.dat rather than combining 1-8XXXX.dat with 1-16XXXX.dat rotated by 22.5 degreees.

• 
• 
• 
• 
• 
• 

To avoid matrix arithmetic problems in some renderers, the third dimension ({y} in the default orientation) of two-dimensional primitives must be given a non-zero scaling factor. LDraw circles are normally formed of 16-sided polygons (hexdecagons) - the regular resolution. For larger elements, where scaling-up of hexadecagons would give too angular an appearance, a series of high resolution primitives based on a 48-sided polygon are available. These may also be used for parts not well suited to a 16-fold symmetry.

These circular elements may be scaled by the same factor in both the {x} and {z} dimensions to make circular elements of greater or less than 1LDu radius. For example

1 16    0 0 0    3 0 0    0 1 0    0 0 3    4-4edge.dat

would generate a circle in the {x,z} plane with a radius of 3LDu.

They may also be scaled asymmetrically in the x and z dimension to make ellipses.

Although the default orientation is in the {x,z} plane the LDraw language allows for these to be transformed

1 16    0 0 0    0 1 0    3 0 0    0 0 3    4-4edge.dat    would generate a circle in the {y,z} plane

1 16    0 0 0    3 0 0    0 0 3    0 1 0    4-4edge.dat    would generate a circle in the {x,y} plane

Two dimensional

n-fedge.dat	Circular line segment
	This suite of primitives are used for edges which comprise an entire or part circle. Currently available primitives: Regular resolution (n-f): 1-16, 1-8, 3-16, 1-4, 5-16, 3-8, 7-16, 2-4, 9-16, 5-8, 11-16, 3-4, 13-16, 7-8, 4-4 High resolution (n-f): 1-48, 1-24, 1-16, 1-12, 5-48, 1-8, 7-48, 1-6, 3-16, 5-24, 11-48, 1-4, 7-24, 5-16, 1-3, 3-8, 19-48, 5-12, 7-16, 11-24, 2-4, 5-8, 2-3, 3-4, 4-4 Low resolution (n-f): 1-4, 2-4, 3-8, 4-4
n-fdisc.dat	Circular disc sector
	This suite of primitives are used for surfaces which comprise an entire or part circle. Currently available primitives: Regular resolution (n-f): 1-16, 1-8, 3-16, 1-4, 5-16, 3-8, 7-16, 2-4, 5-8, 11-16, 3-4, 7-8, 4-4 High resolution (n-f): 1-24, 1-12, 5-48, 1-8, 7-48, 1-6, 3-16, 5-24, 1-4, 1-3, 2-4, 4-4 Low resolution (n-f): 1-4, 2-4, 3-4, 4-4
n-fndis.dat	Inverse of circular disc sector
	This suite of primitives pad their matching n-fdisc.dat primitives out to the bounding square. They are used to integrate circular elements into rectilinear elements. Currently available primitives: Regular resolution (n-f): 1-16, 1-8, 3-16, 1-4, 5-16, 3-8, 7-16, 2-4, 3-4, 7-8, 4-4 High resolution (n-f): 1-24, 1-16, 1-12, 5-48, 1-8, 7-48, 1-6, 3-16, 5-24, 1-4, 1-3, 2-4, 4-4
n-fchrd.dat	Inverse of circular disc sector
	This suite of primitives are used for surfaces which comprise part of a circle enclosed by the arc of its circumference and its chord. Note that the bounding circle in the image is for context only - only the grey segment is generated by the 1-4chrd primitive. Currently available primitives: Regular resolution (n-f): 1-16 (see note), 1-8, 3-16, 1-4, 5-16, 3-8, 7-16, 2-4, 5-8, 3-4, 13-16, 7-8 High resolution (n-f): 1-24, 1-16, 1-12, 5-48, 1-8, 7-48, 1-6, 3-16, 5-24, 11-48, 1-4, 7-24, 5-16, 1-3, 3-8, 19-48, 5-12, 11-24, 2-4 Note: The regular resolution 1-16chrd.dat is a special case, see Primitive Substitution Adapters below for more information
1-16chrd.dat n-fering.dat	Primitive Substitution Adapters
	This suite of primitives are used correct for gaps that form between curved primitives and normal geometry in editors that utilize primitive substitution. This is a special case used on the inside of a curved primitive where it joins geometry that cannot make use of a curved primitive. The chrd files themselves are simply a reference to empty.dat, which under normal circumstances does not draw anything. However, in tools that support primitive substitution, the curved primitive it is attached to would normally in this case create a gap when rendered using more than 16 points to form a circle. In that case, the substituted version of these normally empty primitives would fill in the gap between the curve and the other geometry. To "see" these primitives, the editor in use must utilize primitive substitution. Then one of the following can be done: set the curve quality to a level high enough to see the gaps reappear For LDView 4.4 or later, in the Model Tree dialog, you can search for them (for example, "ering"), and if you have it set to highlight, then when you select one, it will be highlighted in the 3D view. Manually recolor the primitive in question to a color that contrasts with the colors that surround it Note that the bounding circle in the image is for context only - there are no actual geometry producing lines contained in these files. Currently available primitives: Regular resolution (n-f): 1-16chrd, 1-4ering, 1-8ering, 3-16ering, 2-4ering, 4-4ering High resolution (n-f): none
n-ftang.dat	Tangential ring segment
	This suite of primitives are used to pad a 16-sided polygon to a circumscribing 16-sided polygon whose edges are tangential to the inner polygon. Note that the bounding circle in the image is for context only - only the grey segment is generated by the 1-4tang primitive. Currently available primitives: Regular resolution (n-f): 1-16, 1-8, 3-16, 1-4
n-fringr.dat n-frinrr.dat n-ffrinr.dat n-ffrirr.dat nn-ffrir.dat ringr.dat (deprecated name) ringrr.dat (deprecated name)	Circular ring segment
	This suite of primitives are used to generate circular rings or part rings. The numeric suffix r in the filename indicates the inner radius of the ring - the outer radius is 1LDu greater. For example a n-f4-4ring4 primitive would create a ring with an inner radius of 4LDu and an outer radius of 5LDu. Currently available primitives: Regular resolution: r=1 : 1-16rin1, 1-8ring1, 3-16rin1, 1-4ring1, 5-16ring1, 3-8ring1, 7-16rin1, 2-4ring1, 9-16ring1, 5-8ring1, 3-4ring1, 7-8ring1, 4-4ring1 r=2 : 1-16rin2, 1-8ring2, 3-16rin2, 1-4ring2, 5-16rin2, 3-8ring2, 7-16ring2, 2-4ring2, 5-8ring2, 3-4ring2, 7-8ring2, 4-4ring2 r=3 : 1-16rin3, 1-8ring3, 3-16rin3, 1-4ring3, 5-16rin3, 3-8ring3, 7-16rin3, 2-4ring3, 5-8ring3, 3-4ring3, 7-8ring3, 4-4ring3 r=4 : 1-16rin4, 1-8ring4, 3-16rin4, 1-4ring4, 5-16ring4, 3-8ring4, 7-16rin4, 2-4ring4, 5-8ring4, 3-4ring4, 4-4ring4 r=5 : 1-8ring5, 3-16rin5, 1-4ring5, 5-16rin5, 3-8ring5, 2-4ring5, 3-4ring5, 4-4ring5 r=6 : 1-16ring6, 1-8ring6, 3-16rin6, 1-4ring6, 3-8ring6, 7-16ring6, 2-4ring6, 5-8ring6, 3-4ring6, 4-4ring6 r=7 : 1-8ring7, 3-16rin7, 1-4ring7, 5-16ring7, 3-8ring7, 7-16ring7, 2-4ring7, 3-4ring7, 4-4ring7 r=8 : 1-16ring8, 1-8ring8, 3-16rin8, 1-4ring8, 5-16ring8, 3-8ring8, 7-16ring8, 2-4ring8, 3-4ring8, 7-8ring8, 4-4ring8 r=9 : 1-16ring9, 1-8ring9, 3-16rin9, 1-4ring9, 5-16ring9, 3-8ring9, 7-16ring9, 2-4ring9, 3-4ring9, 7-8ring9, 4-4ring9 r=10 : 1-8rin10, 3-16ring10, 1-4rin10, 3-8rin10, 2-4rin10, 5-8ring10, 3-4rin10, 4-4rin10 r=11 : 1-16ring11, 1-8ring11, 3-16ring11, 1-4rin11, 7-16ring11, 2-4rin11, 4-4rin11 r=12 : 1-8ring12, 3-16ring12, 1-4rin12, 5-16ring12, 3-8rin12, 2-4rin12, 7-8rin12, 4-4rin12 r=13 : 1-8ring13, 3-16ring13, 1-4rin13, 5-16ring13, 3-8rin13, 2-4rin13, 4-4rin13 r=14 : 3-16ring14, 1-4rin14, 2-4rin14, 3-4rin14, 4-4rin14 r=15 : 1-8rin15, 3-16ring15, 1-4rin15, 3-8rin15, 2-4rin15, 7-8rin15, 4-4rin15 r=16 : 1-8ring16, 1-4rin16, 3-8rin16, 2-4rin16, 3-4ring16, 7-8rin16, 4-4rin16 r=17 : 1-8rin17, 1-4rin17, 5-16ring17, 3-8ring17, 7-16ring17, 2-4rin17, 4-4rin17 r=18 : 1-16ring18, 1-8rin18, 1-4rin18, 3-8rin18, 2-4rin18, 4-4rin18 r=19 : 1-16ring19, 1-8rin19, 3-16ring19, 1-4rin19, 3-8ring19, 2-4ring19, 3-4ring19, 4-4rin19 r=20 : 1-4rin20, 2-4rin20, 4-4rin20 r=21 : 1-4ring21, 3-8ring21, 4-4rin21 r=22 : 1-16ring22, 3-16ring22, 2-4rin22, 3-4rin22, 4-4rin22 r=23 : 1-16ring23, 1-8rin23, 1-4rin23, 2-4rin23, 4-4rin23 r=24 : 1-16ring24, 3-16ring24, 1-4rin24, 3-8rin24, 2-4rin24, 4-4rin24 r=25 : 1-4ring25, 2-4rin25, 4-4rin25 r=26 : 1-4ring26, 2-4ring26, 4-4rin26 r=27 : 1-8ring27, 4-4ring27 r=28 : 1-8ring28, 1-4rin28, 2-4ring28, 4-4ring28 r=29 : 1-4ring29, 3-8ring29, 2-4ring29, 3-4ring29, 4-4rin29 r=30 : 2-4rin30, 4-4rin30 r=31 : 2-4ring31, 4-4rin31 r=32 : 1-8ring32, 2-4ring32, 4-4rin32 r=33 : 1-8ring33, 1-4ring33, 4-4rin33 r=34 : 1-8ring34, 1-4rin34, 4-4rin34 r=35 : 1-8ring35, 4-4ring35 r=36 : 1-4ring36, 4-4rin36 r=37 : 3-8ring37, 2-4ring37, 4-4rin37 r=38 : 1-4rin38, 4-4rin38 r=39 : 1-16ring39, 1-8rin39, 3-16ring39, 1-4rin39, 7-8rin39, 4-4rin39 r=40 : 1-4ring40, 7-8rin40, 4-4rin40 r=41 : 4-4ring41 r=42 : 2-4ring42 r=43 : 2-4ring43, 4-4rin43 r=44 : 2-4ring44, 4-4rin44 r=45 : 2-4ring45, 4-4rin45 r=46 : 2-4ring46, 4-4rin46 r=47 : 4-4rin47 r=48 : 1-4rin48, 4-4rin48 r=49 : 1-4rin49, 4-4ring49 r=50 : 1-4rin50, 4-4rin50 r=51 : 4-4rin51 r=52 : 2-4rin52, 4-4rin52 r=53 : 3-16ring53 r=55 : 2-4ring55 r=57 : 1-16ring57, 1-4ring57, 4-4rin57 r=61 : 4-4ring61 r=66 : 1-4ring66, 4-4ring66 r=67 : 1-4ring67 r=68 : 4-4ring68 r=70 : 1-16ring70, 1-8ring70, 3-16ring70, 2-4ring70, 4-4ring70 r=71 : 4-4ring71 r=77 : 4-4rin77 r=78 : 4-4rin78 r=79 : 1-4ring79, 4-4rin79 r=80 : 3-16ring80 r=81 : 4-4ring81 r=85 : 4-4rin85 r=88 : 4-4ring88 r=95 : 4-4ring95 r=97 : 4-4ring97 r=101 : 4-4ring101 High resolution: r=1 : 1-24ring1, 1-12rin1, 1-8ring1, 1-6ring1, 3-16ring1, 11-48ring1, 1-4ring1, 5-16ring1, 7-16ring1, 2-4ring1, 4-4ring1.dat r=2 : 1-24ring2, 1-16ring2, 1-12rin2, 5-48ring2, 1-8ring2, 1-6ring2, 3-16ring2, 5-24ring2, 1-4ring2, 1-3ring2, 3-8ring2, 7-16ring2, 2-4ring2, 19-24ring2, 7-8ring2, 4-4ring2 r=3 : 1-24rin3, 1-16rin3, 1-12ring3, 1-8ring3, 7-48ring3, 1-6ring3, 5-24ring3, 1-4ring3, 1-3ring3, 7-16rin3, 2-4ring3, 4-4ring3 r=4 : 1-24rin4, 1-12ring4, 5-48rin4, 1-8ring4, 7-48ring4, 5-24ring4, 1-4ring4, 7-24rin4, 2-4ring4, 4-4ring4 r=5 : 1-24rin5, 1-12rin5, 5-48ring5, 1-8ring5, 7-48rin5, 1-6ring5, 5-24ring5, 1-4ring5, 2-4ring5, 4-4ring5 r=6 : 1-48rin6, 1-24rin6, 1-16ring6, 1-12rin6, 1-8ring6, 1-6ring6, 5-24ring6, 1-4ring6, 2-4ring6, 5-6ring6, 4-4ring6 r=7 : 1-24rin7, 1-16ring7, 1-8ring7, 7-48ring7, 1-6ring7, 3-16rin7, 5-24rin7, 1-4ring7, 2-3ring7, 3-4ring7, 4-4ring7 r=8 : 1-16rin8, 1-12rin8, 1-8ring8, 7-48ring8, 1-6ring8, 3-16rin8, 5-24ring8, 1-4ring8, 11-24ring8, 4-4ring8 r=9 : 1-48rin9, 1-24rin9, 1-12rin9, 5-48rin9, 1-8ring9, 5-24rin9, 11-48ring9, 1-6ring9, 1-4ring9, 1-3ring9, 2-4ring9, 4-4ring9 r=10 : 1-24ring10, 1-16ring10, 1-12ring10, 5-48ring10, 1-8ring10, 7-48ring10, 1-6ring10, 5-24ring10, 1-4rin10, 2-4ring10, 4-4rin10 r=11 : 1-24ring11, 1-16ring11, 1-8ring11, 7-48ring11, 3-16ring11, 1-4rin11, 7-16ring11, 2-4rin11, 4-4rin11 r=12 : 1-12ring12, 1-8ring12, 1-4ring12, 1-6rin12, 2-4rin12, 4-4rin12 r=13 : 1-16ring13, 1-12ring13, 1-8ring13, 1-6rin13, 5-24ring13, 1-4rin13, 5-12ring13, 11-24ring13, 3-4rin13, 4-4rin13 r=14 : 1-24ring14, 1-16ring14, 1-12ring14, 1-8rin14, 1-6rin14, 3-16ring14, 1-4rin14, 3-8ring14, 5-12ring14, 3-4rin14, 4-4rin14 r=15 : 1-48ring15, 1-24ring15, 1-16ring15, 1-12ring15, 1-8ring15, 1-6ring15, 3-16ring15, 5-24ring15, 1-4rin15, 2-4ring15, 4-4rin15 r=16 : 1-16ring16, 1-8rin16, 7-48ring16, 1-6rin16, 1-4rin16, 7-16ring16, 2-4rin16, 3-4rin16, 5-6rin16, 4-4rin16 r=17 : 1-16ring17, 1-12ring17, 1-6rin17, 5-24ring17, 1-4rin17, 1-3rin17, 2-4rin17, 4-4rin17 r=18 : 1-16ring18, 7-48ring18, 1-6rin18, 5-24ring18, 1-4rin18, 4-4rin18 r=19 : 1-24ring19, 1-16ring19, 1-12ring19, 5-48ring19, 1-8ring19, 1-6rin19, 11-48ring19, 1-4rin19, 2-4rin19, 4-4rin19 r=20 : 1-12ring20, 1-8rin20, 5-24ring20, 11-48ring20, 1-4rin20, 4-4rin20 r=21 : 1-16ring21, 11-48ring21, 1-4rin21, 4-4rin21 r=22 : 1-12ring22, 11-48ring22, 1-4rin22, 4-4rin22 r=23 : 1-4rin23 r=24 : 1-24ring24, 1-12ring24, 5-24ring24, 1-4rin24, 4-4rin24 r=25 : 3-16ring25, 1-4rin25, 4-4rin25 r=26 : 1-4rin26, 4-4rin26 r=27 : 1-4rin27, 4-4rin27 r=28 : 1-8rin28, 5-24ring28, 11-48ring28, 1-4ring28, 4-4rin28 r=29 : 1-24ring29, 1-16ring29, 1-12ring29, 5-48ring29, 7-48ring29, 1-6ring29, 3-16ring29, 11-48ring29, 1-4rin29, 5-24ring29, 4-4rin29 r=30 : 1-24ring30, 1-16ring30, 1-4rin30, 3-8ring30, 4-4rin30 r=31 : 1-4rin31, 2-4rin31 r=32 : 5-48ring32, 1-4rin32, 2-4ring32 r=33 : 5-24ring33, 1-4rin33, 4-4rin33 r=34 : 7-48ring34, 5-24ring34, 11-48ring34, 1-4rin34, 2-4ring34, 4-4rin34 r=35 : 1-24ring35, 1-16ring35, 1-8rin35, 5-24ring35, 1-4rin35, 4-4ring35 r=36 : 1-8ring36, 1-4rin36, 1-3ring36, 4-4ring36 r=37 : 1-8ring37, 1-4rin37, 2-4ring37, 4-4rin37 r=38 : 1-12ring38, 1-6ring38, 1-4rin38, 4-4ring38 r=39 : 1-24ring39, 1-16ring39, 1-12ring39, 5-48ring39, 1-8rin39, 7-48ring39, 1-6ring39, 3-16ring39, 1-4rin39, 2-4ring39, 4-4ring39 r=40 : 1-4rin40, 11-48ring40, 2-4ring40 r=41 : 1-8ring41, 1-4rin41, 4-4rin41 r=42 : 1-12ring42, 1-6ring42, 4-4rin42 r=43 : 1-48ring43, 1-16ring43, 1-12ring43, 1-6ring43, 4-4ring43 r=44 : 4-4ring44 r=45 : 1-4rin45, 4-4ring45 r=46 : 1-4ring46 r=47 : 1-6rin47, 1-4ring47, 4-4rin47 r=48 : 7-48ring48, 1-4rin48, 2-4ring48 r=49 : 1-24ring49, 1-16ring49, 1-4ring49, 4-4rin49 r=50 : 1-6rin50, 3-16ring50, 4-4rin50 r=51 : 1-4rin51 r=52 : 11-24ring52, 4-4rin52 r=53 : 1-8ring53, 3-16ring53, 4-4rin53 r=54 : 4-4rin54 r=55 : 2-4ring55 r=56 : 1-12ring56, 1-8rin56 r=57 : 1-4ring57, 4-4ring57 r=59 : 1-24ring59, 1-16ring59, 1-12ring59 r=60 : 1-24ring60, 1-16ring60 r=63 : 1-4rin63 r=64 : 1-4rin64 r=65 : 1-4rin65 r=69 : 5-24ring69 r=70 : 1-4rin70 r=71 : 1-4rin71, 4-4ring71 r=77 : 4-4ring77 r=78 : 1-12ring78 r=79 : 1-4ring79 r=80 : 7-48ring80, 1-6ring80 r=81 : 4-4ring81 r=82 : 1-4rin82 r=83 : 1-4rin83 r=84 : 1-8ring84 r=85 : 4-4ring85 r=88 : 4-4ring88 r=90 : 11-48ring90 r=95 : 2-4ring95 r=96 : 1-4ring96 r=97 : 4-4rin97 r=99 : 1-6ring99, 4-4ring99 r=100 : 1-24ring100, 4-4ring100 r=130 : 4-4ring130 r=160 : 2-4ring160 r=179 : 1-4ring179 r=240 : 2-4ring240 Low resolution: r=2 : 2-4ring2, 4-4ring2 r=3 : 1-4ring3, 4-4ring3 r=6 : 4-4ring6 r=7 : 4-4ring7 r=11 : 4-4ring11
n-faring.dat	Circular adaptor ring segment
	This suite of primitives are used to interface between high resolution (48-segment) circular primitives and normal resolution (16-segment) circluar primitives. Currently available primitives: Regular resolution (n-faring): 4-4 High resolution (n-faring): 1-4

Three dimensional

n-fcyli.dat n-fcyli2.dat	Circular cylinder
	This suite of primitives are used to generate cylinders or part cylinders. These are provided in two forms - with conditional lines (n-fcyli) or without conditional lines (n-fcyli2). In almost all circumstances the "cyli" version should be used. The "cyli2" versions are for very special cases and their use for the rounded corners of stickers is no longer appropriate. Currently available primitives - with conditional lines: Regular resolution (n-fcyli): 1-16, 1-8, 3-16, 1-4, 5-16, 3-8, 7-16, 2-4, 5-8, 11-16, 3-4, 7-8, 4-4 High resolution (n-fcyli): 1-48, 1-24, 1-16, 1-12, 5-48, 1-8, 7-48, 1-6, 3-16, 5-24, 1-4, 7-24, 1-3, 3-8, 5-12, 7-16, 11-24, 2-4, 5-8, 2-3, 3-4, 7-8, 4-4 Currently available primitives - without conditional lines: Regular resolution (n-fcyli2): 3-16, 1-4, 5-16, 2-4, 3-8, 4-4 High resolution (n-fcyli2): 1-4, 2-4, 4-4
n-fcylo.dat	Circular cylinder with Open End
	This suite of primitives are used to generate cylinders or part cylinders with edges around the lower and upper surfaces. Currently available primitives: Regular resolution (n-fcylo): 1-16, 1-8, 3-16, 1-4, 5-16, 3-8, 7-16, 2-4, 5-8, 3-4, 7-8, 4-4 High resolution (n-fcylo): 1-48, 1-24, 1-16, 1-12, 5-48, 1-8, 7-48, 3-16, 5-24, 1-4, 1-3, 2-4, 4-4
n-fcylc.dat n-fcylc2.dat n-fcylc3.dat	Circular cylinder with Closed End
	This suite of primitives are used to generate cylinders or part cylinders with the upper surface closed. Currently available primitives - with conditional lines and top edge line: Regular resolution (n-fcylc): 1-4, 2-4, 3-4, 4-4 High resolution (n-fcylc): 2-4, 4-4 Currently available primitives - without conditional lines or top or bottom edge line: Regular resolution (n-fcylc2): 1-4, 4-4 High resolution (n-fcylc2): 4-4 Currently available primitives - with conditional lines, but without top and bottom edge lines: Regular resolution (n-fcylc3): 1-4, 4-4 High resolution (n-fcylc3):